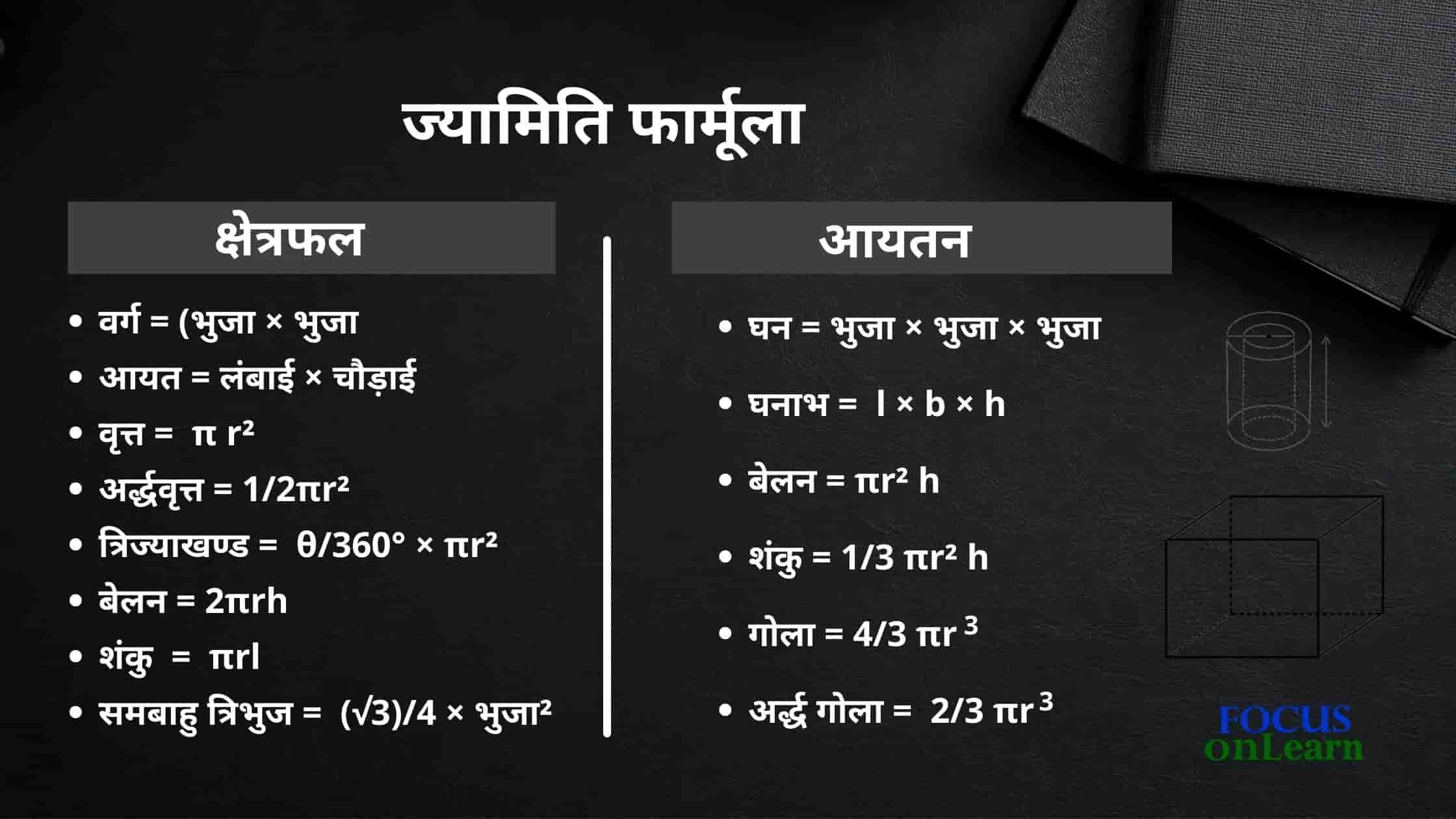
ज्यामिति स्वतंत्र रूप से प्रारंभिक आकृतियों की लंबाई, क्षेत्र और मात्रा को व्यावहारिक तरीके से मापने के लिए इसका प्रयोग किया जाता था. लेकिन आज के दौर में इसका प्रचालन गणित के अधिकतर कार्यो में होता है. इसलिए इसका अध्ययन Geometry Formula in Hindi के माध्यम से करेंगे.
सामान्यतः ज्यामिति को दो अलग- अलग भागों में विभाजित किया जा सकता है. पहला, समतल ज्यामिति और दूसरा, ठोस ज्यामिति. समतल ज्यामिति में वृत्त, त्रिभुज, आयत, वर्ग इत्यादि जैसी आकृतियां शामिल होती है. जबकि, सॉलिड ज्योमेट्री या ठोस ज्यामिति में विभिन्न प्रकार के ज्यामितीय आकृतियों की लंबाई, परिधि, क्षेत्रफल आयतन इत्यादि शामिल होती है. इन आकृतियों की गणना करने के लिए Geometry Formula का प्रयोग किया जाता है.
गणितीय ज्यामिति अन्य टॉपिक से थोड़ा कठिन प्रतीत होता है क्योंकि इसमें कुछ ऐसे चिन्ह और फार्मूला होते है जिन्हें सरलता से समझना मुश्किल होता है. लेकिन यहाँ ज्यामिति से सम्बंधित सभी आवश्यक फार्मूला को उपलब्ध कराया गया है जो दैनिक जीवन एवं बोर्ड एग्जाम के दृष्टिकोण से आवश्यक है.
इसमें कुछ ऐसे भी सूत्र है जिससे आप पहले से परिचित है और कुछ ऐसे है जिसका प्रयोग आप केवल प्रश्न हल करने के लिए करते है. कठिन लगने वाले ज्यामिति फार्मूला यहाँ इस प्रकार प्रदर्शित किया गया है जिसे आप सरलता से याद कर सकते है.
| वर्ग का परिभाषा एवं क्षेत्रफल | घन का क्षेत्रफल |
| आयत का विशेष क्षेत्रफल | समानान्तर चतुर्भुज का क्षेत्रफल |
| समलम्ब चतुर्भुज का क्षेत्रफल | समचतुर्भुज का क्षेत्रफल |
| त्रिभुज का क्षेत्रफल | शंकु का क्षेत्रफल |
Table of Contents
सामान्यतः ज्यामिति गणित की एक ऐसी शाखा है जिसके अंतर्गत बिंदुओं, रेखाओं, तलों, ठोस चीजों के गुण, मापन तथा इसके स्वभाव, का अध्ययन किया जाता है. गणितज्ञ इसे भूमिति भी कहते है क्योंकि इसकी उत्पति के समय इसका प्रयोग भूमि मापन के लिए किया जाता था.
इसके सम्बन्ध में और भी महत्वपूर्ण तथ्य उपलब्ध है जिसका अध्ययन ज्यामिति फार्मूला के अनुसार करेंगे.
| वर्ग की परिमाप | 4 × a |
| वर्ग का क्षेत्रफल | (भुजा × भुजा) = a² |
| वर्ग का क्षेत्रफल | ½ × (विकर्णो का गुणनफल) = ½ × d 2 |
| आयत का परिमाप | 2(लम्बाई + चौड़ाई) |
| घन का आयतन | भुजा × भुजा × भुजा = a 3 |
| घन का परिमाप | 4 a² |
| घन का विकर्ण | √3 × भुजा |
| आयत का क्षेत्रफल | लंबाई × चौड़ाई |
| आयत का विकर्ण | √(लंबाई² + चौड़ाई²) |
| समलम्ब चतुर्भुज का क्षेत्रफल | ½ (समान्तर भुजाओं का योग x ऊंचाई) |
| समलम्ब चतुर्भुज का परिमाप | P = a + b+ c + d |
| विषमकोण चतुर्भुज का क्षेत्रफल | ½ × दोनों विकर्णो का गुणनफल |
| समचतुर्भुज की परिमाप | 4 × एक भुजा |
| समचतुर्भुज का सम्पबंध | (AC)² + (BD)² = 4a² |
| चक्रीय चतुर्भुज का क्षेत्रफल | √[s(s-a) (s-b) (s – c) (s – c)] |
| चक्रीय चतुर्भुज का परिमाप | ½ ( a + b + c + d ) |
| वृत्त का क्षेत्रफल | π r² |
| वृताकार वलय का क्षेत्रफल | π (R 2 – r 2 ) |
| अर्द्धवृत्त का क्षेत्रफल | 1/2πr² |
| त्रिज्याखण्ड का क्षेत्रफल | θ/360° × πr² |
| चाप की लम्बाई | θ/360° × 2πr |
| वृतखण्ड का क्षेत्रफल | (πθ/360° – 1/2 sinθ)r² |
| घनाभ का आयतन | l × b × h |
| घनाभ का परिमाप | 2(l + b) × h |
| घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल | 2(lb + bh + hl) |
| कमरें के चारों दीवारों का क्षेत्रफल | 2h ( l + b ) |
| बेलन का आयतन | πr 2 h |
| बेलन का वक्रपृष्ठ का क्षेत्रफल | 2πrh |
| बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल | 2πr ( h + r ) |
| शंकु का आयतन | 1/3 πr 2 h |
| शंकु के वक्र पृष्ठ का क्षेत्रफल | πrl |
| गोले का वक्रपृष्ठ का क्षेत्रफल | 4πr 2 |
| गोला का आयतन | 4/3 πr 3 |
| अर्द्ध गोला का आयतन | 2/3 πr 3 |
ज्यामिति में प्रयोग किए जाने वाले सामान्य फार्मूला का यह लिस्ट है. जिसका प्रयोग हमेशा प्रश्न हल करने के लिए किया जाता है. व्यावहारिक प्रयोग के लिए इसका इस्तेमाल किया जा सकता है.
कुछ ऐसे ज्यामिति फार्मूला उपलब्ध है जिसका प्रयोग केवल टॉप कम्पटीशन परीक्षा, थ्योरम और बोर्ड एग्जाम के प्रशों को हल करने के लिए होता है. जिसका लिस्ट निचे नियमबद्ध तरीके से अंकित किया गया है.
| समबाहु त्रिभुज का क्षेत्रफल | (√3)/4 × भुजा 2 |
| समबाहु त्रिभुज का शीर्षलम्ब | (√3)/4 × भुजा |
| समद्विबाहु त्रिभुज का क्षेत्रफल | a / 4 b √ (4b² – a²) |
| विषमबहु त्रिभुज का क्षेत्रफल | √ [ s(s – a)(s – b)(s – c) ] |
| हिरोन का सूत्र | √ [ s(s – a)(s – b)(s – c) ] |
| किसी अर्द्ध गोला के सम्पूर्ण पृष्ठ का क्षेत्रफल | 3 πr 2 |
| गोलीय शेल के सम्पूर्ण पृष्ठ का क्षेत्रफल | 4/3 π ( R 2 – r 2 ) |
| लम्बवृतीय शंकु के सम्पूर्ण पृष्ठ का क्षेत्रफल | πr ( l + r ) |
| लम्बवृतीय बेलन की ऊँचाई | (बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल / 2πr) – r |
| खोखले बेलन में लगीधातु का आयतन | πh (R 2 – r 2 ) |
| ढक्कनरहित टंकी का क्षेत्रफल | 2h ( l + b ) + lb |
| घनाभ का विकर्ण | √(l² + b² + h²) |
| घन का एक किनारा | 3 √आयतन |
| वृतखण्ड की परिमिति | (L + πrθ)/180° , जहाँ L = जीवा की लम्बाई |
Geometry Formula in Hindi से सम्बंधित सभी आवश्यक फार्मूला यहाँ दिया गया है जिसका प्रयोग आप व्यक्ति लाभ और प्रश्न हल करने के लिए करते है. यदि इस टॉपिक में कोई संदेह हो, तो हमें कमेंट करे. हम आपकी प्रशों का उत्तर अवश्य देंगे.
गणित से सम्बंधित महत्वपूर्ण फार्मूला
| बेलन का आयतन | घन का आयतन |
| शंकु का आयतन | समानान्तर श्रेढ़ी फार्मूला |
| द्विघात समीकरण फार्मूला | क्लास 10th त्रिकोंमिति फार्मूला |
| घनाभ का आयतन | निर्देशांक ज्यामिति फार्मूला एवं परिभाषा |
ज्यामिति गणित की एक शाखा है जो गुणों और बिंदुओं, रेखाओं, कोणों, सतहों एव ठोस पदार्थों से मिल कर बना है.
ज्यमितीय के तिन प्रकार निम्न है, पहला समतल ज्यामिति, दूसरा ठोस ज्यामिति, और तीसरा गोलाकार ज्यामिति.
| Whatsapp Group | Join |
| Telegram channel | Join |